Inhaltsverzeichnis
Integralrechnung - Schnittflächen
Erklärung des Problems
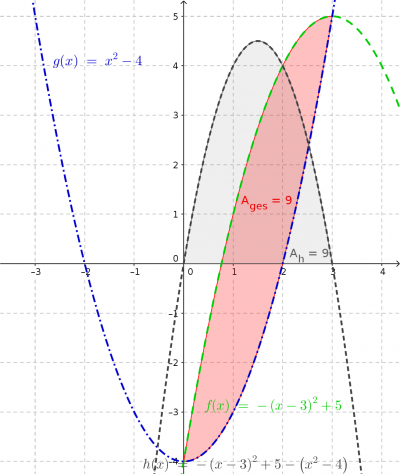
Neben der reinen Flächenberechnung unterhalb eines Funktionsgraphen, gibt es auch die Fragestellung nach der von zwei Funktionsgraphen eingeschlossenen Fläche. Diese Flächen werden durch die Schnittstellen begrenzt. Das folgende Bilder verdeutlicht dies.
Bezug zum Buch Cornelsen
| Thema | Seite | Bemerkung |
|---|---|---|
| Fläche zwischen zwei Funktionen | 225 | Theorie/Einführung in Thema |
| Fläche zwischen zwei Funktionen | 226 | Theorie/Erklärung einfaches Beispiel |
| Mehrere eingeschlossene Fläche zwischen zwei Funktionen | 227 | Theorie/Vertiefung |
| Vorgehensweise grüner Kasten | 228 | Merkregel/Zusammenfassung |
| Übung 1. orange | 228 | Einfache Übung |
| Übung 2. orange | 228 | Praxisaufgabe* |
*: ähnlich wie in der Abschlussprüfung
Vorgehensweise zur Berechnung von Schnittflächen
Um die Schnittflächen zu berechnen werden als Integrationsgrenzen die Schnittstellen benötigt. Diese können durch Gleichsetzung der beiden Funktionen $f(x)$ und $g(x)$ ermittelt werden. Es gilt:
$f(x_s)=g(x_s)$ oder $h(x)=f(x_s)-g(x_s)=0$
Die Funktion $h(x)$ dient als Hilfsfunktion. Damit reduziert sich die Schnittstellenbestimmung der beiden Funktionen auf eine Nullstellenbestimmung der Hilfsfunktion $h(x)=0$.
Durch Anwendung des Hauptsatzes der Integralrechnung lässt sich weiterhin folgender Zusammenhang definieren:
$\int ( f(x) - g(x)) \cdot dx = \int h(x) \cdot dx$
Jeweils in den Grenzen der Schnittstellen. D.h. es genügt die von $h(x)$ eingeschlossenen Flächen von Nullstelle zu Nullstelle betragsmäßig aufzunehmen addieren, umziehen Schnittflächen zwischen $f(x)$ und $g(x)$ zu berechnen. Damit wurde das Problem der Schnittflächenberechnung auf das bekannte Problem der Flächenberechnung einer von einem Funktionsgraphen begrenzten Fläche reduziert.
Folgende Schritte sind demnach notwendig:
- Ermittlung der Hilfsfunktion $h(x) = f(x) - g(x)$
- Berechnung der Nullstellen von h(x)
- Integration von $h(x)$ von Nullstelle (= Schnittstelle) zu Nullstelle mit Betrag(!) (vergleiche Flächenberechnung)
Aufgaben zu Schnittstellenbestimmung
Berechnen Sie jeweils die durch die beiden Funktionsgraphen der Funktionen $f(x)$ und $g(x)$ eingeschlossenen Flächen.
| a) $f(x) = x^2-9$ und $g(x) = -x^2 + 9$ | b) $f(x) = -x^2+ 2 x + 3$ und $g(x) = -x +3$ |
| c) $f(x) = 4 x - x^3$ und $g(x) = 2x-x^2$ | d) $f(x) = x^3 + x^2 -2$ und $g(x) = x^3 +x$ |
Lösungen (unsortiert)
| $A = 4,5$ | $A = 0,42 + 2,67 = 3,08$ | $A = 4,5$ | $A = 72$ |
⇒ Weitere Informationen zum oben beschriebenen Thema finden Sie hier:
| Buch | Verlag | Auflage | Druck | Seiten |
|---|---|---|---|---|
| Mathematik Technik Fachhochschulreife | Cornelsen | 1. Auflage | 1. Druck 2014 | 225 - 228 |
| Mathematik Technik Fachhochschulreife | Cornelsen | 1. Auflage | 2. Druck 2015 |