Inhaltsverzeichnis
Arbeitsblatt
Arbeitsblatt als PDF (inkl. Tabelle mit Größeneinheiten) DOWNLOAD
Signal
Definition: Ein Signal ist die physikalische Darstellung von Nachrichten oder Daten. 1)
Analoges Signal
Definition: Ein analoges Signal kann kontinuierlich jeden beliebige Werte zwischen einem Minimum und einem Maximum annehmen.
Beispiel einer Sinus-Schwingung
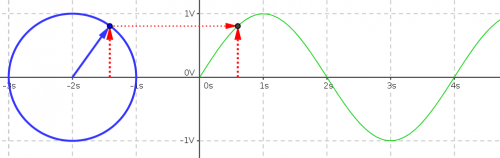 Das gezeigte Bild ist ein „sinusförmiger Spannungsverlauf“, dh die Spannung verläuft über die Zeit gemäß den Sinuswerten beim durchlaufen eines Kreises. Die maximale Spannung (positiv bzw. negativ) wird auch Amplitude A genannt. Die „Geschwindigkeit“ mit der einmal alle Sinuswerte durchlaufen werden, nennt man Frequenz f. Die Periodendauer T gibt an, wie viel Zeit für einen vollständigen Umlauf des Kreises benötigt wird. Je schneller der Kreis umlaufen wird, umso höher ist die Frequenz f und umso kürzer die Zeit T.
Das gezeigte Bild ist ein „sinusförmiger Spannungsverlauf“, dh die Spannung verläuft über die Zeit gemäß den Sinuswerten beim durchlaufen eines Kreises. Die maximale Spannung (positiv bzw. negativ) wird auch Amplitude A genannt. Die „Geschwindigkeit“ mit der einmal alle Sinuswerte durchlaufen werden, nennt man Frequenz f. Die Periodendauer T gibt an, wie viel Zeit für einen vollständigen Umlauf des Kreises benötigt wird. Je schneller der Kreis umlaufen wird, umso höher ist die Frequenz f und umso kürzer die Zeit T.
| Frequenz |
|---|
| |
| |
| mit T der Periodendauer in [s] und f der Frequenz in [Hz] ( |
Übung 1: Analoge Signale (Frequenz, Amplitude, Periodendauer)
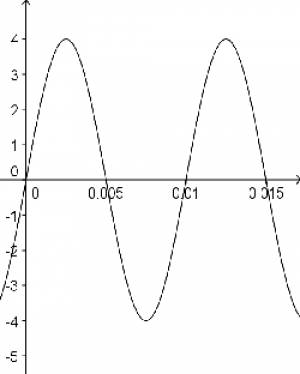
Lesen Sie in der Skizze die Periodendauer T ab und errechnen Sie daraus die Frequenz f. Bestimmen Sie die Amplitude A.
Beispiel 1:
| Größe | Zahlenwert |
|---|---|
| T = | |
| f = | |
| A = |
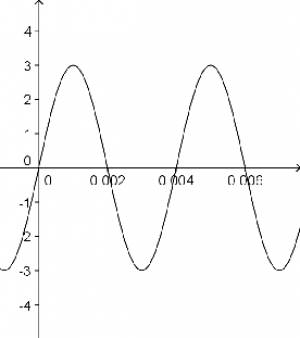
Beispiel 2:
| Größe | Zahlenwert |
|---|---|
| T = | |
| f = | |
| A = |
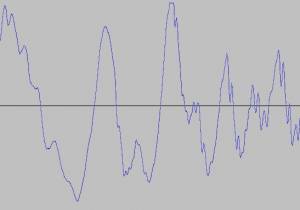
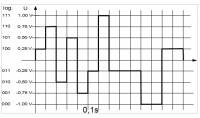
In der Realität kommen selten reine Sinusschwingungen vor. Meist handelt es sich um ein „Gemisch“ unterschiedlicher Frequenzen. Man kann sich dieses Gemisch als die Summe einzelner sinusförmiger Schwingungen mit unterschiedlichen Amplituden vorstellen. Das folgende Bild stellt ein solches Gemisch dar, welches man beispielsweise an einem Lautsprecher als Spannungsverlauf aufzeichnen könnte.
Defnition: Digitales Signal
Ein digitales Signal kann nur zu diskreten 2) Zeitpunkten, quantisierte 3) Werte zwischen einem Minimum und einem Maximum annehmen.
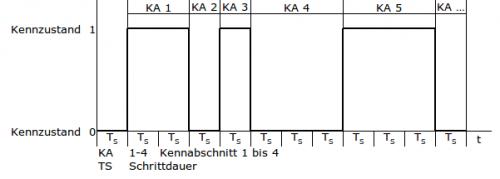
Das digitales Signal kann nach der Schrittdauer TS seinen Kennzustand ändern. Die Zeitspanne, während der das Signal sich nicht ändert, ist der Kennabschnitt KA. In diesem Beispiel sind genau zwei Kennzustände zulässig. Ein solches Signal nennt man binär4). Die möglichen Informationen 0 und 1 haben die Einheit Bit (binary digit).
| Schrittrate |
|---|
| |
| mit der Schrittrate vS in [Bd] Schritt pro Sekunde |
| und der Schrittdauer TS in [s] |
Informationsgehalt
Definition: Der Informationsgehalt einer Datenmenge wird in der Maßeinheit Bit (binary digit) angegeben. Ein Bit kann die Werte 0 oder 1 annehmen. Ein Bit kann aus der Anzahl der Kennzustände errechnet werden:
| Informationsgehalt |
|---|
| |
| mit Anzahl Bit b in [Bit/Schritt] |
| und Anzahl der Kennzustände n |
Übertragungsrate
Definition: Die Übertragungsrate ist die Anzahl von Bits pro Schrittdauer TS.
| Übertragungsrate |
|---|
| |
| mit der Übertragunsrate vD in [ |
| mit der Anzahl Bit b in [ |
| und der Schrittdauer TS in [s] |
Definition: Zusammenhang zwischen Schrittrate und Übertragungsrate Je mehr Bit pro Sekunde übertragen werden, umso höher ist die Übertragungsrate bei gleicher Schrittdauer.
| Übertragungsrate |
|---|
| |
| mit der Übertragunsrate vD in [ |
| mit der Schrittrate vS in [Bd] |
| mit der Anzahl Bit b in [ |
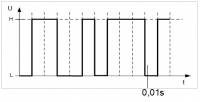
Übung 2: Digitale Signale (Kennzustände, Schrittrate)
a) Wie viele Kennzustände haben die Signale?
b) Lesen Sie die Schrittdauer TS ab.
c) Errechnen Sie die Schrittrate vS.
d) Wie viele Zustandsänderungen wären bei den folgenden Schrittdauern TS in einer Sekunde möglich?
| Schrittdauer TS | Zustandsänderungen |
|---|---|
| 0,0005s | |
| 0,01s | |
| 25 ms |
e) Gegeben ist vS = 0,2 Bd und folgende Bitfolge: 0011000101001 bei b=2.
Zeichnen Sie das Signal in ein geeignetes Raster.
Wie groß ist die Schrittdauer?
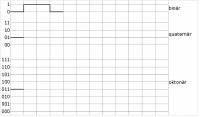
Übung 3: Digitale Signale (Kennzustände, Informationsgehalt, Schrittrate, Übertragungsrate)
a) Zeichnen Sie die gegebene Bitfolge als binär, quaternär und oktonär codiertes Signal. Die Bitfolge 011010010111 soll binär, quaternär und oktonär codiert werden.
b) Worin unterscheiden sich die drei Signale?
Übung 4: Zusammenfassung digitale Signale (Kennzustände, Informationsgehalt, Schrittrate, Übertragungsrate)
a) Die maximale Schrittrate der betrachten Signale beträgt 1,2 kBaud. Welche Übertragungsraten liegen vor, wenn 4, 16, 64 oder 512 Kennzustände verwendet werden?
| Kennzustände | Informationsgehalt | Übertragungsrate |
|---|---|---|
| 4 | ||
| 16 | ||
| 64 | ||
| 512 |
b) Wie ändert sich die Schrittrate bei konstanter Übertragungsrate, wenn die Anzahl der Kennzustände erhöht wird?
c) Wie viele Bit werden pro Schritt benötigt, wenn bei einer Schrittrate von 2kBd in 4 Sekunden 40.000 Bit übertragen werden sollen?
d) Es sollen 240.000 Bit bei oktonärer Codierung übertragen werden. Wie lange dauert dies bei einer Schrittdauer von 0,001s? Und wie groß ist die Übertragungsrate?
e) Ein Bild hat die Auflösung von 1920×1080 Bildpunkten bei einer Farbtiefe von 32 Bit pro Bildpunkt. Das Bild soll über eine Datenleitung mit einer Übertragungsrate von 16000 Bit/s übertragen werden. Wie lange wird die Übertragung dauern?
f) Wie viele bit pro Schritt werden benötigt, wenn bei einer Schrittrate von 10kBd in 3 Sekunden die Datenmenge von 120.000bit übertragen werden sollen? Wie viele Kennzustände werden dabei eingesetzt?
LÖSUNGEN Aufgabe 4 (unsortiert): Die Lösungen sind für jede Teilaufgabe und ggf. Unteraufgabe gemischt aufgeführt. Z.B. a) 8 Teilaufgaben → 8 Lösungen
- Sie wird kleiner
- 4 bit/Schritt
- 2 bit/Schritt
- 4147,2s (69,12min 1h9min)
- 4,8kbit/s
- 2,4kbit/s
- 3 kbit/s
- 9 bit/Schritt
- 6 bit/Schritt
- 7,2kbit/s
- 4 bit/Schritt
- 5 bit/Schritt
- 10,8kbit/s
- 80s
- 16 Kennzustände