Polynomdivision
Mit Hilfe der Polynomdivision lassen sich gezielt Nullstellen einer ganzrationalen Funktion (sinnvoll ab n=3 also dritten Grades1))abspalten. Alle restlichen Nullstellen liegen im sogenannten Restpolynom.
<m> f(x) : (x - x_{N}) = r(x) </m>
<m> r(x)</m> ist hierbei das Restpolynom in dem unter Umständen noch weitere Nullstellen enthalten sein können. D.h. das Restpolynom wird wie schon f(x) nach Nullstellen untersucht.
Beispiel zur Durchführung einer Polynomdivision:
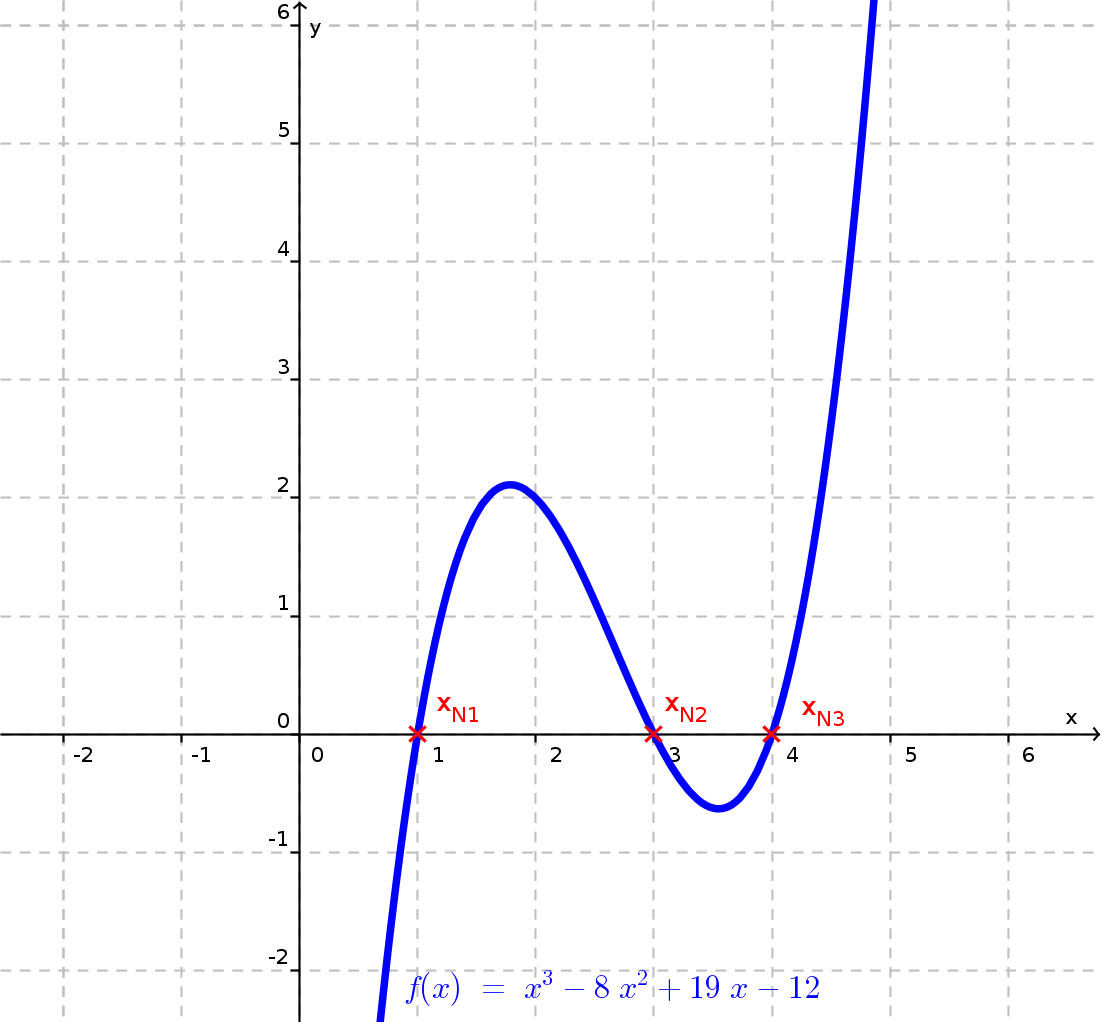
Gegeben ist die Funktion <m> f(x) = x^3 - 8 x^2 + 19 x -12 </m>
Durch Probe wurde die Nullstelle x=4 gefunden.
Damit ergibt sich folgende Polynomdivision:

Das Restpolynom ist hier 2. Grades also quadratisch und kann mittels pq-Formel auf weitere Nullstellen untersucht werden (s. unterer Teil der Rechnung).
Hier der Graph zur obigen Funktion: