Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Extremwertaufgaben
Beispiel Rechteckfläche
Es soll ein rechteckiger Sandkasten gebaut werden. Der Sandkasten soll flächenmäßig so groß wie möglich werden. Zur Verfügung stehen zwei 8 m lange Bretter. Wie lang müssen die Kanten gewählt werden, damit die Grundfläche des Sandkastens maximal wird?
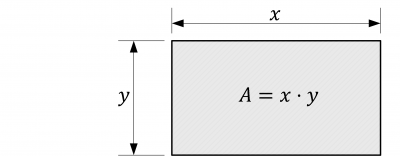
1. Skizze erstellen
2. Aufstellen der Hauptbedingung/Zielfunktion
Welche Größe soll hier „optimiert“ werden? Die Fläche! Demnach ergibt sich die Hauptbedingung zu: $A=x \cdot y $
3. Aufstellen der Nebenbedingung/Randbedingung
Welche weiteren Informationen enthält die Aufgabenstellung, um Unbekannte zu eliminieren? Es stehen zwei Bretter je 8 m zur Verfügung. Der Umfang beträgt demnach 16 m!
$\Rightarrow$ Nebenbedingung: $2~x+2~y=16$ $\Rightarrow$ $x+y=8$ $\Rightarrow$ $y=8-x$
4. Hauptfunktion/Zielfunktion mittels Nebenbedingung/Randbedingung vereinfachen
Einsetzen der Nebenbedingung in die Hauptbedingung führt zu:
$A(x)=x \cdot (8-x)=8x-x^2$
5. Extremum (Optimum) ermitteln
Notwendige Bedingung: $A'(x)=0$
$A'(x)=8-2x=0 \Rightarrow x=4$
Hinreichende Bedingung: $A''(x)\neq0$
$A''(4)=-2 <0 \Rightarrow$ Es handelt sich um ein Maximum $\checkmark$
6. Lösung ermitteln
Durch einsetzen von $x$ in die Nebenbedingung kann nun noch $y$ bestimmt werden:
$y=8-x=8-4=4 $
Antwort: Die größte Fläche resultiert wenn als Grundfläche ein Quadrat mit den Kantenlängen $x=y=4$ gewählt wird.
Beispiel Dosenoptimierung
Es soll Suppe mit dem Volumen V = 800 ml in einer Dose verpackt werden. Dabei soll der Blechverbrauch minimal werden. Bestimmen Sie das optimale Verhältnis zwischen Höhe $h$ und Radius $r$ der Dose.
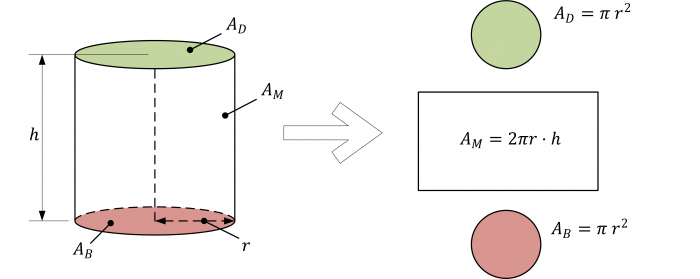
1. Skizze erstellen
2. Aufstellen der Hauptbedingung/Zielfunktion
Welche Größe soll hier „optimiert“ werden? Die Oberfläche! Demnach ergibt sich die Hauptbedingung zu: $A=2 \cdot \pi ~ r^2+2 \pi~r \cdot h$
3. Aufstellen der Nebenbedingung/Randbedingung
Welche weiteren Informationen enthält die Aufgabenstellung, um Unbekannte zu eliminieren? Das Volumen der Dose soll 800 ml betragen!
$\Rightarrow$ Nebenbedingung: $V=0,8~l=0,8~dm^3=\pi~ r^2 \cdot h$
$\Rightarrow$ $h=\frac{0,8~dm^3}{\pi ~r^2}$
4. Hauptfunktion/Zielfunktion mittels Nebenbedingung/Randbedingung vereinfachen
Einsetzen der Nebenbedingung in die Hauptbedingung führt zu:
$A=2 \cdot \pi ~ r^2+2 \pi~r \cdot \frac{0,8~dm^3}{\pi ~r^2} = 2 \cdot \pi ~ r^2+ \frac{1,6~dm^3}{r} = 2 \cdot \pi ~ r^2+ 1,6~dm^3 \cdot r^{-1}$
5. Extremum (Optimum) ermitteln
Notwendige Bedingung: $A'(r)=0$
$A'(r)=4 ~ \pi ~ r-\frac{1,6}{r^2}=0 \Rightarrow 4 ~ \pi \ r = \frac{1,6}{r^2} \Rightarrow r^3=\frac{1,6}{4~\pi} \Rightarrow r=\sqrt[3]{\frac{1,6}{4~ \pi}} \approx 0,5~dm $
Hinreichende Bedingung: $A''(r)\neq0$
$A'(r)=4 ~ \pi ~ r-1,6 \cdot r^{-2} \Rightarrow A''(r)=4 ~ \pi +2 \cdot 1,6 \cdot r^{-3} =4 ~ \pi +2 \frac{1,6}{r^3}$
$\Rightarrow A''(0,5)=4 ~ \pi +2 \frac{1,6}{0,5^3} \approx 38,2 >0 \Rightarrow$ Es handelt sich um ein Minimum $\checkmark$
6. Lösung ermitteln
Durch einsetzen von $r$ in die Nebenbedingung kann nun noch $h$ bestimmt werden:
$h(r)=\frac{0,8}{\pi ~r^2} \Rightarrow h(0,5)=\frac{0,8}{\pi ~0,5^2} \approx 1,02~dm $
Antwort: Bei einem Radius von $r=0,5~dm=5~cm$ und einer Höhe von $h=1,02~dm=10,2~cm$ resultiert für eine Dose mit einem Volumen von 800 ml der minimale Materialverbrauch.
Kostenoptimierung
Die Gewinnes eins Unternehmens sollen optimiert werden. Bei einer entsprechenden Analyse konnten die Kosten K als Funktion
<m> K(x)= 0,04 x^3 - 0,64 x^2 + 3,6 x + 2 </m>
Das Unternehmen stellt große Mengen her, daher stellt x die Menge in 10.000 Stück dar und die Kosten K sind in 10.000 € dargestellt.
Der Erlös 1) kann in Abhängigkeit der verkauften Waren x als Erlösfunktion E(x) dargestellt werden:
<m> E(x)= - 0,16 x^2 + 2,76 x </m>
a) Wie viel Stück Ware sollten produziert werden, damit der Gewinn maximal wird?
b) Wie groß ist der Maximalgewinn?
c) Wie groß ist der Erlös pro Stück beim Maximalgewinn?
Lösungsskizze: a)
- Gewinn $G(x) = E(x) - K(x)$ (Gewinn= Erlös - Kosten)
- $G'(x)$ und $G''(x)$ bestimmen
- Maximum mittels $G'(x_E)=0$ berechnen
- Mit $G''(x)$ überprüfen
- $Menge_max=x_E \cdot 10.000 St$ gemeint ist die Menge (Stück) an Waren
b)
- $Maximalgewinn= G(x_E) \cdot 10.000 €$ (10.000€ s. Normierung für K(x)
c)
- Gesamterlös$ = E(x_E) \cdot 10.000 €$ für die gesamte Menge in €
- Stückerlös$ = \frac{Gesamterlös }{x_E \cdot 10.000}$
Aufgaben zu Extremwertaufgaben aus dem Buch
Die folgenden Aufgaben sind nach Themen sortiert und können im Buch „Mathematik Technik Fachhochschulreife“ Cornelsen Verlag 1. Auflage, 1. Druck 2014 gefunden werden.
| Thema | Seite | Aufgabe | Lösung |
|---|---|---|---|
| Extremwertberechung | 186f | Erklärung | |
| Extremwertberechung Vorgehensweise | 189 | Erklärung | |
| Aufgaben | 190 | A1, A2 | siehe S. 423 |
| Aufgabe | 192 | A1 | $a=5~;~b=5~;~d=7,07$ |
| Aufgabe | 192 | A2 | In der Aufgabenstellung muss es gleichschenkliges Dreieck heißen! $g=40~;~a=40~;~h=34,64$ |
| Aufgabe | 192 | A3 | $a=10,95~;~b=10,95$ |
| Aufgabe | 192 | A4 | $r=0,7~;~h=0,7$ |
| Aufgabe | 192 | A5 | $x=4~;~A_{max}=8m^2$ ACHTUNG: Fehler in der Skizze (s.u.) |
| Aufgabe | 192 | A6 | $x\approx 3,3~;~ k(3,3) \approx 103941,13$ |
| Aufgabe | 193 | A12 | a) $C(4|\frac{8}{3})$; b) $l_1=4~\text{LE}, ~l_2=\frac{8}{3}~\text{LE}$ |
| Aufgabe | 193 | A13 | a) $u=1,5~;~v=2,53125$; b) $A_{max} \approx 3,8~\text{FE} $; … |
| A13 | c) max: $u\approx 1,15~\text{&}~v \approx 2,99$ $;$ min: $u\approx 2,38~\text{&}~v=0$; … | ||
| A13 | d) $U_{max}=8,29~\text{LE}; U_{min}=4,76~\text{LE}$ |
/* | Aufgaben | 192ff | A5 A6 A12 A13 u.a. | *
Korrektur Skizze: S.192 A5 (Kiosk)
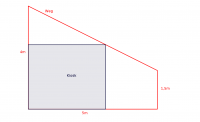
Für „Mathematik Technik Fachhochschulreife“ Cornelsen Verlag 1. Auflage, 2. Druck 2015 gilt:
| Thema | Seite | Aufgabe | Lösung |
|---|---|---|---|
| Extremwertberechung | 186f | Erklärung | |
| Extremwertberechung Vorgehensweise | 189 | Erklärung | |
| Aufgaben | 190 | A1, A2 | siehe S. 423 |
| Aufgabe | 192 | A1 | $a=5~;~b=5~;~d=7,07$ |
| Aufgabe | 192 | A2 | $g=40~;~a=40~;~h=34,64$ |
| Aufgabe | 192 | A3 | $a=10,95~;~b=10,95$ |
| Aufgabe | 192 | A4 | $r=0,7~;~h=0,7$ |
| Aufgabe | 192 | A5 | $x=4~;~A_{max}=8m^2$ |
| Aufgabe | 192 | A6 | $x\approx 3,3~;~ k(3,3) \approx 103941,13$ |
| Aufgabe | 193 | A12 | a) $C(4|\frac{8}{3})$; b) $l_1=4~\text{LE}, ~l_2=\frac{8}{3}~\text{LE}$ |
| Aufgabe | 193 | A13 | a) $u=1,5~;~v=2,53125$; b) $A_{max} \approx 3,8~\text{FE} $; … |
| 193 | A13 | c) max: $u\approx 1,15~\text{&}~v \approx 2,99$ $;$ min: $u\approx 2,38~\text{&}~v=0$; … | |
| 193 | A13 | d) $U_{max}=8,29~\text{LE}; U_{min}=4,76~\text{LE}$ |
/* | Aufgaben | 192ff | A5 A6 A12 A13 u.a. | *
Weitere Extremwertaufgaben
Weitere Aufgaben Pfeffer 7. Auflage S. 226!