Ein bestimmtes Integral ermittelt aus dem beiden Teilflächen, die von einer Funktion f(x) und der x-Achse eingeschlossen werden, den Flächeninhalt zwischen zwei Grenzen a und b.

Skizze:

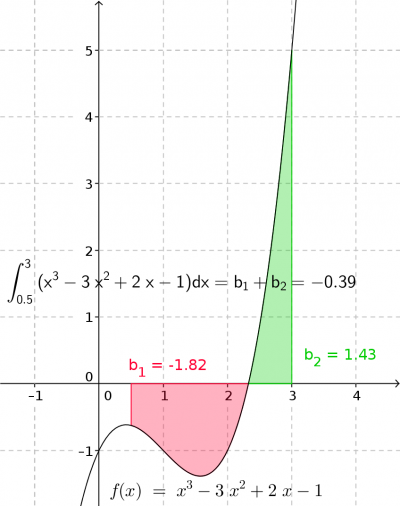
Die Funktion lautet <m>f(x) =x^3 - 2 x^2 + 2 x- 1</m> und die Integralgrenzen wurde zu a=0,5 und b=3 festgelegt.

Die linke (rote) Fläche liegt unterhalb der x-Achse und liefert daher einen negativen Flächenbeitrag. Die rechte (grüne) Fläche liefert liegt oberhalb der x-Achse und liefert daher einen positiven Flächenbeitrag. Zusammen ergibt sich ein negativer Wert, da die rote Fläche größer ist als die grüne.

Man kann dies auch mit einer „Gewinn/Verlust“-Rechnung als Ananlogie gleichsetzen. Dabei wäre die rote Fläche der Verlust und die grüne Fläche der Gewinn. Das Integral liefert als den Gesamtverlust/-gewinn. Hier: Gesamtverlust in Höhe von -0,39 FE. Die innerhalb des Integrals liegende Nullstelle spielt bei der Berechnung keine Rolle.

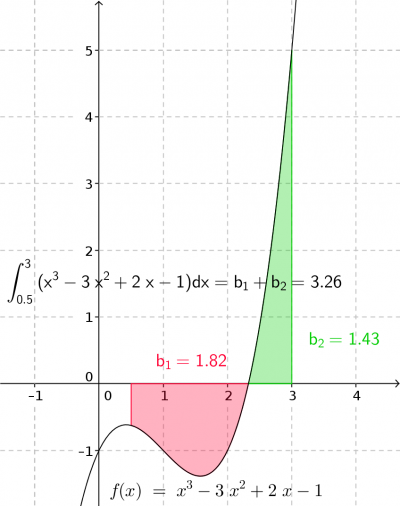
Wird im gleichen Bespiel nach der eingeschlossenen Fläche zwischen f(x) und der x-Achse gefragt, so ist nach den absoluten (positiven) Flächen gefragt. In diesem Fall müssen die einzelnen Flächen (hier: <m>b_1</m> und <m>b_2</m> ) als positive Werte ermittelt und aufaddiert werden.

Die Rechnung dazu sieht ähnlich aus. Hinweis: Die Nullstelle wurde mittels Geogebra ermittelt. Hier kommen die bekannten Verfahren zum Einsatz (Probe, Horner-Schema, Polynom-Division, pq-Formel)