Bei der Bestimmung der Stammfunktion erstehen unendlich viele Stammfunktionen, die durch eine Konstante C zum Ausdruck kommen.

$\int f(x) dx = F(x) +C$

Für C kann jede beliebige Zahl aus R eingesetzt werden.

Wie kann man nun eine bestimmte Stammfunktion ermitteln?

Betrachtet man eine beliebige integrierbare Funktion f(x), dann kann man die dazugehörende Stammfunktionen F(x) durch das unbestimmte Integral bestimmen.

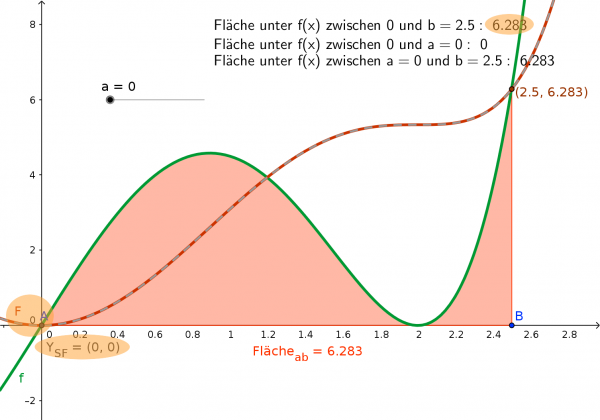
(grüne Kurve: $f(x)=0,5x^5 - 4x^3 + 8x$ rote Kurve:$F(x) = \frac{1}{12} x^6 – x^4 + 4 x^2+C$ )

Zur besseren Verdeutlichung wurde ein Integral von a=0 bis b=2,5 (rosa hinterlegt) eingezeichnet. Die entsprechenden Flächen sind oberhalb abzulesen (Für das Intervall [0;2,5] → 6,283) Dabei ist zunächst C=0 wie man am Durchlauf der roten Kurve durch den Ursprung (0;0) erkennt. Durch Verändern der linke unteren Integrationsgrenze (a=0) auf den Wert a=0.6 (willkürlich). Hierdurch verschiebt sich die Kurve der Stammfunktion F(x) um genau den Wert 1,314 nach Unten (vgl. y-Achsenabschnitt von F(x)= -1,314 und damit Integrationskonstante C = -1,314 mit dem Wert der Fläche im Intervall [0;0,6]=1,314). Es ergibt sich also exakt der Wert der Fläche im Intervall [0;a=0,6] als neuer negativer y-Achsenabschnitt bzw. C bei der Stammfunktion F(x). s. orange Markierung in der nächsten Abbildung:

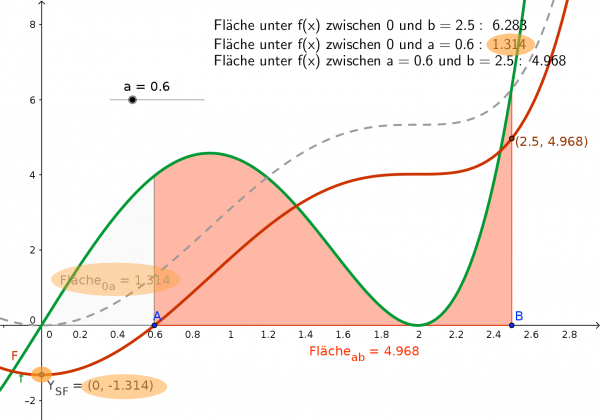
Wie man an der gestrichelten Kurve (ursprünglichen Stammfunktion) sieht, ist die Form der Stammfunktion nicht verändert, sondern nur die Lage. Man kann auch umgekehrt über die Verschiebung der Stammfunktion die Integrationskonstante C ermitteln.

Gegeben ist ein Punkt $ P(x_P, y_P)$, durch den die Stammfunktion laufen soll. Gesucht ist nun die Integrationskonstante C, die dies ermöglicht. Durch folgenden Ansatz kann C ermittelt werden.

Ansatz:
$F(x_P) +C = y_P$
(Einsetzen des Punktes P in die Stammfunktion)

Anschliessend wird nach C aufgelöst.

Gegeben: $f(x)=- 3 x^2 + 4 x + 5$

Gesucht: Berechnen Sie die Integrationskonstante C der Stammfunktion F(x), damit F(x) durch den Punkt P(1|4) verläuft.

Ansatz:
1. Zunächst wird die Stammfunktion F(x) nach den bekannten Integrationsregeln bestimmt:
$F(x)= - x^3+2x^2+5x+C$

2. Koordinaten von P in F(x) einsetzen, dann nach C auflösen:
$F(1)+C = 4$
$\Leftrightarrow F(1) = - (1)^3 + 2 \cdot (1)^2 + 5 \cdot (1)+C = 4$
$\Leftrightarrow C = 4 + 1 - 2 -5 = -2$

3. Ergebnis:
$F(x)= - x^3+2x^2+5x \boldsymbol{-2}$