kopfload - Lad Dein Hirn auf!

Bitte beachten Sie, dass diese Aufgaben NUR zur Übung dienen. Sie bilden nicht alle Klausurthemen ab. Die Lösungen lassen sich leicht mit Geogebra überprüfen.

1. Stellen Sie die Funktionsgleichung der nach unten geöffneten Normalparabel auf, die durch die Punkte P(1|2) und Q(-1|-3) verläuft.
2. Zeigen Sie rechnerisch, dass der Punkt P (1|1) nicht auf dem Graphen der Funktion <m> ~ f(x)= -x^2 – 1 </m> liegt.
3. Ermitteln Sie die Funktionsgleichung der quadratischen Funktion, deren Scheitelpunkt an der Stelle x=-1 liegt, deren Stauchung -0,5 beträgt und die durch den Punkt P(1|1) verläuft.
4. Geben Sie die Funktionsgleichung der quadratischen Funktion f an, die als Normalparabel um -2 in x-Richtung und +3 in y-Richtung verschoben ist, sowie eine Streckung von 4 erfahren hat.
5. Geben Sie die Koordinaten des Scheitelpunktes an und sowie den Koeffizienten des linearen Gliedes für die folgenden Funktionen.

5.a) <m> ~f_a(x)= - (x- ~{1 / 2} )^2 </m>

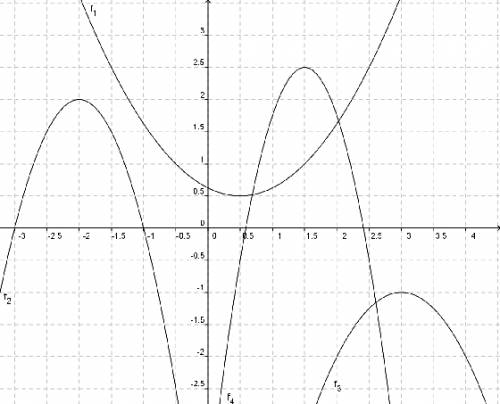
5.b) <m> ~f_b(x)= 1/2 ( x +~ 3/2 )^2 – ~1/3 </m>	

6. Geben Sie die Funktionsgleichungen der abgebildeten Funktionsgraphen an.