Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Einführung zu quadratischen Funktionen
Quardatische Funktionen zählen zu den ganzrationalen Funktionen, die sich aus unterschiedlichen Potenzen von x zusammensetzen. Bei quadratischen Funktionen ist die höchste vorkommende Potenz x^2.
Allgemeine Form einer quadratischen Funktion
Die allgemeine Form einer quadratische Funktion sieht wie folgt aus.
<m>f(x) = a_2 x^2 + a_1 x + a_0</m>
Mit <m> a_2 <> 0 </m> <m> a_1, a_0 in R </m>
Diese Form eignet sich besonders, um z.B. Nullstellen der Funktion f(x) zu ermitteln.
Scheitelpunktform einer quadratischen Funktion
Die Scheitelpunktform einer quadratische Funktion sieht wie folgt aus.
<m>f(x) = a_2( x - x_S)^2 +y_S</m>
Mit <m> a_2 <> 0 </m> <m> x_S, y_S in R </m>
Diese Form eignet sich besonders, um z.B. Nullstellen der Funktion f(x) zu ermitteln.
Mit dem Geogebra-Arbeitsblatt1) lässt sich untersuchen, wie der Scheitelpunkt aus der Gleichung abgelesen werden kann und für eine Skizze verwendet werden kann.
Das letzte Geogebra-Arbeitsblatt enthält drei Parabeln an denen die jeweiligen Scheitelpunkte abgelesen werden sollen.
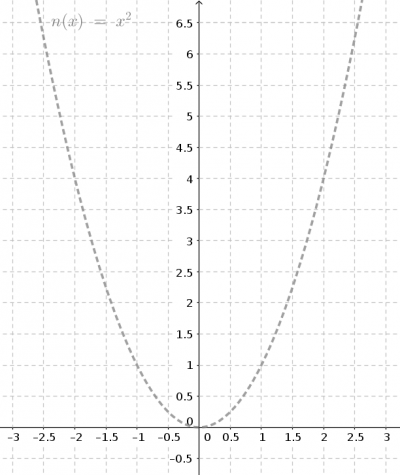
Normalparabel
Als Normalparabel wird die Parabel bezeichnet, die durch den Ursprung geht und bei der der Streck-/Stauchungsfaktor <m>a_2 = 1</m> ist. Mit dem Geogebra-Arbeitsblatt lässt sich untersuchen, wie eine Parabel in Scheitelpunktform durch die Parameter beeinflusst werden. Als Referenz ist die Normalparabel in grau gestrichelt eingezeichnet.