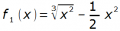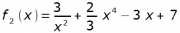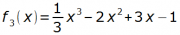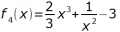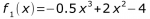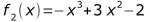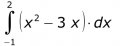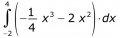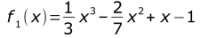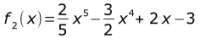Inhaltsverzeichnis
Musterlösung zu Integralrechnung
Im folgenden Dokument werden Vorgehensweisen zu einigen Integralaufgaben aufgeführt:
Vorgehensweise für Integralrechnung
Gemischte Aufgaben zur Integralrechnung
1. Bestimmen Sie die Stammfunktionen zu den gegebenen Funktionen.
2. Bestimmen Sie das bestimmte Integral zwischen -1 und 3 der folgenden Funktionen.
3. Berechnen Sie folgende Integrale.
4. Bestimmen Sie die Fläche A, die von der x-Achse und dem Graphen der
Funktion 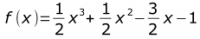 eingeschlossen wird.
eingeschlossen wird.
5. Geben Sie die Stammfunktionen der folgenden Funktionen an, sodass die Graphen der Stammfunktionen jeweils durch den Punkt P(1 | 0) verlaufen.
6. Bestimmen Sie die Schnittpunkte der folgenden Funktionen und ermitteln Sie die durch die Graphen der beiden Funktionen begrenzte Fläche A.
(HINWEIS: Häufig wird hier noch eine Skizze verlangt, nachdem die notwendigen Punkte ermittelt wurden. Bei diesen beiden Funktionen ist dies nicht möglich, da die Nullstellen von f(x) und g(x) nicht ganzzahlig sind.)
Lösungen zu folgenden Aufgaben (Pfeffer 7.Auflage)
- S. 237 A6.2 c)
- S. 242 A6.12 d)
- S. 242 A6.10 a)
- S. 243 A6.14 e)
- S. 247 A6.27 a) Winkelhalbierende f(x)=x